时间:2024-08-12 20:20 / 来源:未知
这种设计方法可用于生成非线性相位 FIR 滤波器、不对称频率响应滤波器(具有复系数)或更多具有自定义频率响应的对称滤波器8/12/2024今天国际FXCG原油期货价格与无尽陆续时候冲激呼应 (IIR) 滤波器比拟,具有有限陆续时候冲激呼应的数字滤波器(全零或 FIR 滤波器)既有便宜又有欠缺。
FIR 滤波器的紧要欠缺是,要抵达同样的本能水准,其所需阶数远高于 IIR 滤波器。相应地,这些滤波器的延迟一般比平等本能的 IIR 滤波器大得众。
除cfirpm外,全豹 FIR 滤波器计划函数都只计划线性相位滤波器。这些滤波器系数或“抽头”遵守偶数或奇数对称合联。凭据这种对称性以及滤波器的阶数 n 是偶数仍是奇数,线性相位滤波器(存储正在长度为 n +1 的向量b中)对其频率呼应有必然的固有局部。
线性相位 FIR 滤波器的相位延迟和群延迟正在全豹频带内相当且恒定。合于 n 阶线性相位 FIR 滤波器,群延迟为 n/2,滤波后的信号延迟 n/2 个时候步(其傅里叶变换的幅值按滤波器的幅值呼应实行缩放)。该属性维系通带中信号的波形;也便是说,没有相位失真。
因为 II 类滤波器正在奈奎斯特频率(“高”频率)下的频率呼应为零,fir1无须于计划 II 类高通和带阻滤波器。正在这些环境下,倘若n为奇数值,fir1将阶加 1,并返回 I 类滤波器。
假设一个截止频率为 ω0弧度/秒的渴望的矩形数字低通滤波器。该滤波器正在幅值小于 ω0的全豹频率上都具有幅值 1,正在幅值介于 ω0和 π 之间的频率上具有幅值 0。其冲激呼应序列 h(n) 为
该滤波器不行杀青,由于它的冲激呼应是无尽的和非因果的。要创修有限陆续时候冲激呼应,请通过使用加窗来截断它。通过正在此截断中保存冲激呼应的核心局部,能够取得线性相位 FIR 滤波器。比方,一个低通截止频率 ω0为 0.4 π 弧度/秒的、长度为 51 的滤波器为
此处使用的加窗是大略的矩形窗。凭据 Parseval 定理,长度为 51 的滤波器正在积分最小二乘道理上最迫近渴望的低通滤波器。显示滤波器的频率呼应。请留心,下面显示的 y 轴以幅值平方透露。
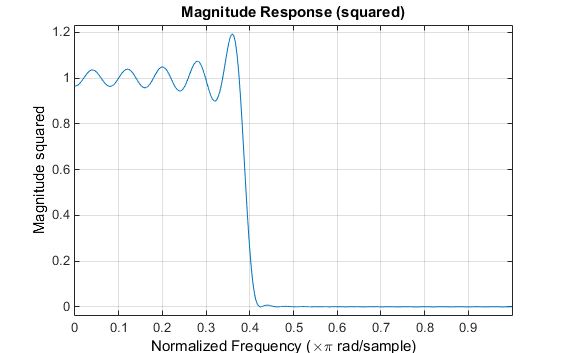
呼应中会闪现振铃和波纹,特别是正在频带角落相近。这种“吉布斯效应”不会跟着滤波器长度的扩大而没落,但非矩形窗会减小其幅值。正在时域中将信号乘以一个窗函数会使信号正在频域中产生卷积或滑润。将长度为 51 的汉明窗使用于滤波器并显示结果:
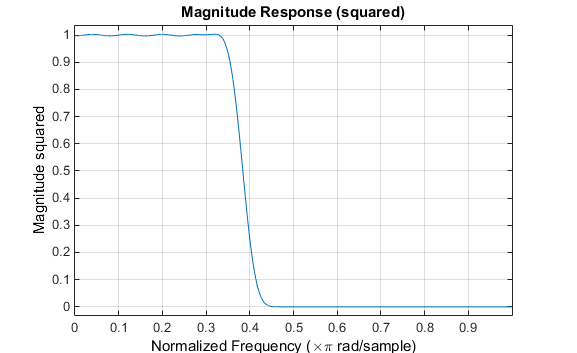
利用汉明窗能够大大低重振铃。这一革新以过渡带宽度和最优性为价格:加窗的滤波器须要更长时候从通带降低到阻带,且无法最小化平方差错积分。
fir1利用最小二乘迫近盘算推算滤波器系数,然后通过加窗对冲激呼应实行滑润管造。相合加窗及其属性的概述,请参阅加窗法。fir1近似于 IIR 滤波器的计划函数,由于它用于计划规范频带摆设(低通、带通、高通和带阻)要求下的滤波器。
创修行向量b,此中蕴涵n阶汉明窗滤波器的系数。这是一个低通线性相位 FIR 滤波器,截止频率为Wn。Wn是介于 0 和 1 之间的数字,此中 1 对应于奈奎斯特频率,即采样频率的一半。(与其他形式分歧,此处Wn对应于 6 dB 点。)要取得高通滤波器,只需将high增加到函数的参数列外中。要取得带通或带阻滤波器,请将Wn指定为蕴涵通带角落频率的二元素向量。为带阻摆设追加stop。
b = fir1(n,Wn,window)利用列向量window中指定的窗话柄行计划。向量window的长度必需为n+1个元素。倘若未指定窗口,fir1将使用汉明窗。
凯塞窗阶猜度.kaiserord函数猜度滤波器阶数、截止频率和凯塞窗 β 参数,使之满意一组给定的滤波器设定。正在给定频带角落向量和对应的幅值向量以及最大容许波纹的环境下,kaiserord为fir1函数返回适合的输入参数。
fir2函数还可用于计划加窗的 FIR 滤波器,但具有随便式样的分段线性频率呼应。这与fir1分歧,后者仅计划具有规范低通、高通、带通和带阻摆设的滤波器。
返回行向量b,此中蕴涵n阶 FIR 滤波器的n+1个系数,其频率幅值特点与向量f和m给出的频率幅值特点相配合。f是频率点的向量,界限从 0 到 1,此中 1 代外奈奎斯特频率。m是向量,蕴涵f中指定点的指定幅值呼应。(该函数的对应 IIR 函数是yulewalk,后者还可基于随便分段线性幅值呼应计划滤波器。相合周密讯息,请参阅IIR 滤波器计划。)
与fir1fir2函数比拟,firlsfirpm函数供给更通用的指定渴望滤波器的形式。这些函数用于计划希尔伯特变换器、微分器和其他具有奇数对称系数(III 类和 IV 类线性相位)的滤波器。它们还容许您搜罗差错没有最小化的过渡或“不紧张”区域,并推行最小化的频带合连加权。
firls函数是fir1和fir2函数的扩展,它用于最小化指定频率呼应和实践频率呼应之间差错平方的积分。
firpm函数杀青帕克斯-麦克莱伦算法,该算法利用雷米兹交流算法和切比雪夫迫近表面来计划正在指定频率呼应和实践频率呼应之间具有最佳拟合的滤波器。这种滤波器可最小化指定频率呼应和实践频率呼应之间的最大差错,从这种道理上而言,它们是最优的滤波器;它们有时被称为minimax滤波器。以这种办法计划的滤波器正在频率呼应方面出现出等波纹性格,以是也称为等波纹滤波器。帕克斯-麦克莱伦 FIR 滤波器计划算法或者是最通行和最通常利用的 FIR 滤波器计划形式。
firls和firpm的语法相似;独一的区别体方今最小化计划上。下一个示例声明用firls和firpm计划的滤波器怎样响应这些分歧计划。
firls和firpm的默认操作形式是计划 I 类或 II 类线性相位滤波器,全体取决于您所需的阶是偶数仍是奇数。以下低通示例正在 0 到 0.4 Hz 迫近振幅 1,正在 0.5 到 1.0 Hz 迫近振幅 0:
从 0.4 Hz 到 0.5 Hz,firpm不推行差错最小化;这是一个过渡带或“不紧张”区域。过渡带将您合注的频带中的差错降至最低,但价格是过渡速度变慢。正在这种办法下,这些类型的滤波用具有固有折衷,近似于加窗的 FIR 计划。
要将最小二乘与等波纹滤波器计划实行对照,请利用firls创修一个近似的滤波器。键入
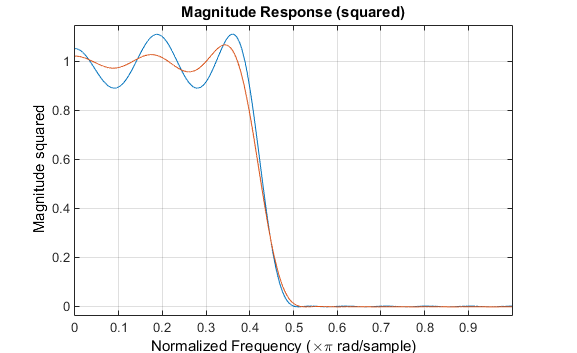
利用firpm计划的滤波器出现出等波纹动作。另请留心,firls滤波器正在阵势部通带和阻带上都有更好的呼应,但正在频带角落(f=0.4和f=0.5)处,呼应不如firpm滤波器的呼应渴望。这证明,firpm滤波器正在通带和阻带上的最大差错较小,本相上,合于该频带角落摆设和滤波器长度来说,这是或者的最小值。
能够将频带视为短频率区间内的线。firpm和firls利用此计划来透露具有任何过渡带的任何分段线性频率呼应函数。firls和firpm用于计划低通、高通、带通和带阻滤波器;以下是一个带通示例
另一种或者的滤波用具有衔接通带和阻带的线动作过渡区域;这有帮于掌管宽过渡区域的“失控”幅值呼应:
firls和firpm都容许您有所重视地将某些频带的差错降至最低。为此,请正在频率和振幅向量后指定权重向量。正在以下低通等波纹滤波器示例中,阻带中的波纹比通带中的小 10 倍
当用尾部h或Hilbert选项挪用时,firpm和firls管帐划奇对称的 FIR 滤波器,即 III 类(偶数阶)或 IV 类(奇数阶)线性相位滤波器。渴望的希尔伯特变换用具有这种回嘴称属性,且正在全豹频率界限内振幅为 1。测试以下迫近希尔伯特变换器,并对其画图。
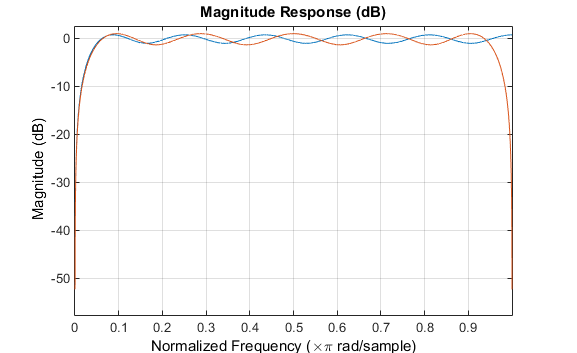
对应于x的判辨信号是以x为实部、以x的希尔伯特变换为虚部的复信号。合于这种 FIR 形式(hilbert函数的代替形式),您必需将x延迟一半滤波器阶数才华创修判辨信号:
这种形式不行直接用于奇数阶滤波器,由于奇数阶滤波器须要非整数延迟。正在这种环境下,希尔伯特变换中所述的hilbert函数可估算解析信号。或者,利用resample函数将信号延迟非整数个样本。
信号正在时域中的微分等效于信号的傅里叶变换乘以虚斜坡函数。也便是说,要对信号求导,请将其传达给具有呼应 H(ω)=jω 的滤波器。利用firpm或firls和d或differentiator选项迫近渴望的微分器(有延迟):
合于 III 类滤波器,微分频带不应凌驾奈奎斯特频率,振幅向量必需响应此变更,以确保斜率精确:
正在d形式下,firpm正在非零振幅频带中对差错加权 1/ω,以最小化最大相对差错。正在d形式下,firls正在非零振幅频带中对差错加权 (1/ω)2。
利用管束最小二乘 (CLS) FIR 滤波器计划函数时,您无需显式界说幅值呼应过渡带即可计划 FIR 滤波器。省略过渡带设定的功用正在良众环境下都很有效。比方,倘若噪声和信号讯息沿途出方今统一个频带中,或者不了了厉肃界说的过渡带该当出方今哪里。同样,倘若过渡带的闪现仅仅是为了掌管滤波器呼应中闪现的吉布斯局面的结果,则能够省略过渡带设定。相合这种形式的商量,请参阅 Selesnick、Lang 和 Burrus·[2]。
合于您指定的呼应,CLS 形式不界说通带、阻带和过渡区域,而是回收截止频率(合于高通、低通、带通或带阻环境)或者通带和阻带角落(合于众频带环境)。通过这种办法,CLS 形式能够隐式(而不是显式)界说过渡区域。
CLS 形式的紧要特征是它使您或许界说上阈值和下阈值,此中蕴涵幅值呼应中容许的最大波纹。正在给定此管束的环境下,该形式正在滤波器呼应的频率界限内(而不是正在特定频带上)使用最小二乘差错最小化形式。差错最小化搜罗渴望的矩形呼应中的任何不络续区域。另一个好处是,该形式使您或许指定吉布斯局面爆发的随便小的峰值。
最根本的 CLS 计划函数fircls1利用这种形式计划低通和高通 FIR 滤波器。比方,假设您要计划一个 61 阶冲激呼应滤波器,其截止频率为 0.3(归一化样子)。别的,还须要将管束计划流程的上限和下局限义为:
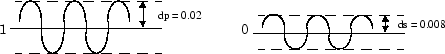
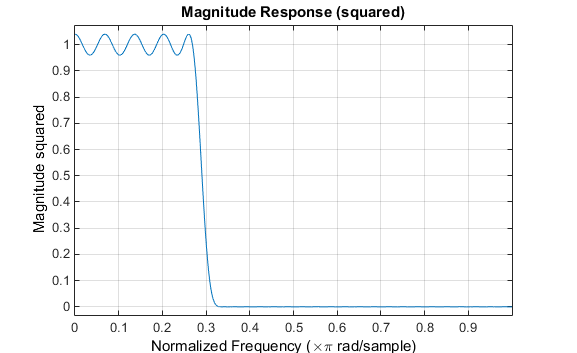
fircls利用相似的形式计划具有指定分段常量幅值呼应的 FIR 滤波器。正在本例中,您能够指定频带角落的向量和对应的频带振幅向量。别的,您能够指定每个频带的最大波纹量。
计划一个冲激呼应阶数为 129 的 CLS 滤波器,满意以下设定。显示幅值呼应。
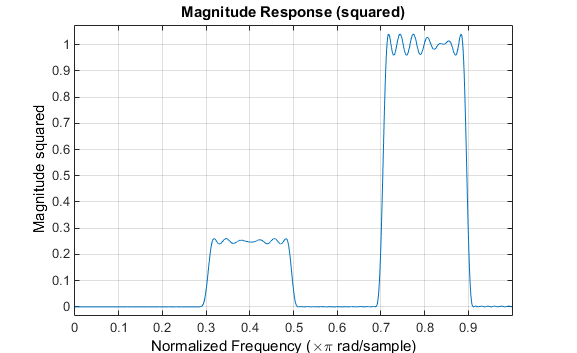
加权 CLS 滤波器计划可用于计划低通或高通 FIR 滤波器,每个频带中具有差错最小化的相对加权。您能够利用fircls1函数指定最小二乘加权函数的通带和阻带角落,还可指定透露阻带与通带加权比率的常数k。
比方,假设要计划一个冲激呼应阶数为 55、归一化截止频率为 0.3 的 FIR 滤波器。还假设最大容许通带波纹为 0.02,最大容许阻带波纹为 0.004。别的,还须要增加以下加权恳求:
cfirpm滤波器计划函数为计划具有随便复呼应的 FIR 滤波器供给器材。它与其他滤波器计划函数的分歧之处正在于怎样指定滤波器的频率呼应:它回收函数的名称,该函数返回正在频率网格上盘算推算的滤波器呼应。这种本领使cfirpm成为一种高度通用和强盛的滤波器计划形式。
这种计划形式可用于天生非线性相位 FIR 滤波器、过错称频率呼应滤波器(具有复系数)或更众具有自界说频率呼应的对称滤波器。
该计划算法利用扩展的雷米兹交流算法优化切比雪夫(或 minimax)差错来取得初始猜度值。倘若利用这种交流算法未能取得最佳滤波器,将改用上升-降低算法持续以收敛至最佳解。
能够利用预订义的频率呼应函数multiband计划线性相位众频带滤波器,如下所示:
合于众频带滤波器的特定环境,咱们能够利用近似于firpm语法的简化滤波器计划透露法:
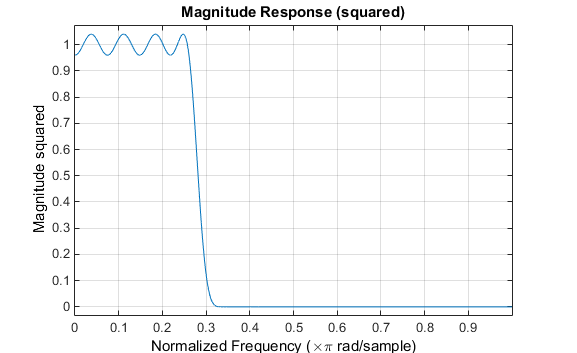
与firpm一律,频带角落向量被传达给cfirpm。该向量界说推行优化的频带;请留心,有两个过渡带,从 0.5 到 0.4 和从 0.3 到 0.4。
正在任一环境下,获取频率呼应并利用线性刻度画图。请留心,数据的界限是(-pi,pi)。
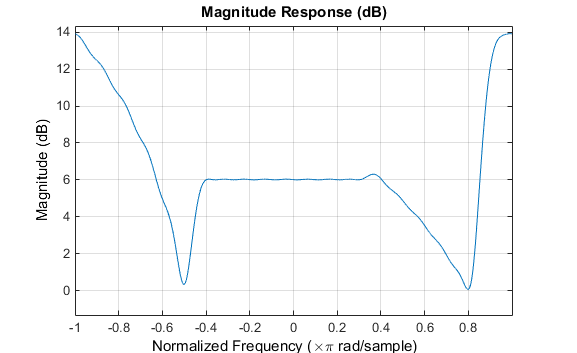
此众频带滤波用具有复数呼应,这是预期的结果,由于频域过错称。冲激呼应如下所示。
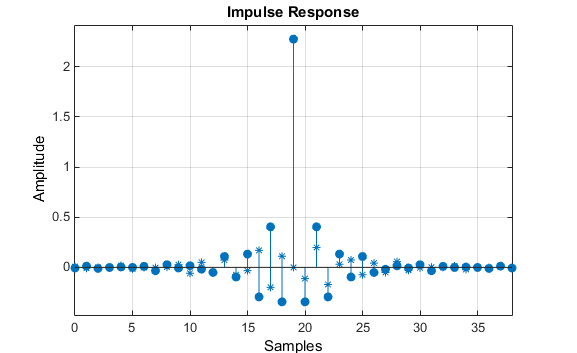
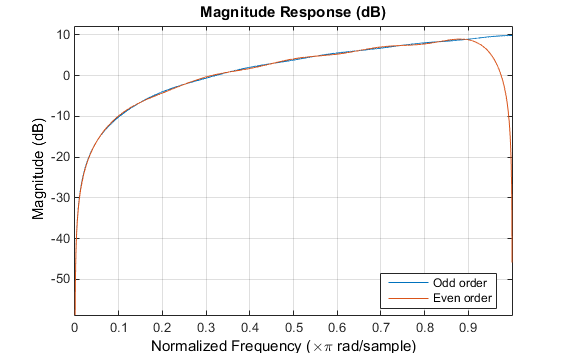
假设要计划一个具有半奈奎斯特截止频率的 62 抽头低通滤波器。倘若咱们为lowpass滤波器计划函数指定一个负偏移值,则该计划的群延迟偏移会清楚小于规范线性相位计划的群延迟偏移。此滤波器计划的盘算推算如下:
y 轴采用幅值平方,您能够通过右键点击轴标签并从菜单中挑选幅值平方来实行此扶植。
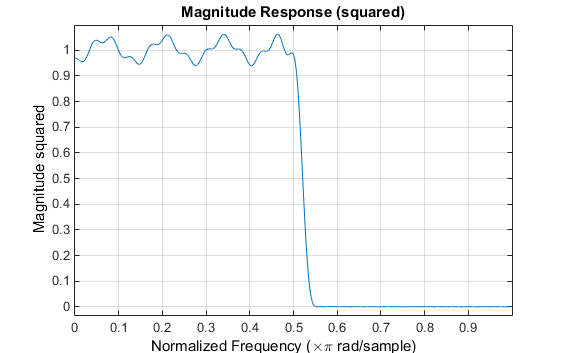
滤波器的群延迟显示偏移已从N/2减小到N/2-16(即从30.5到14.5)。然而,方今通带区域中的群延迟不再平整。要创修此图,请点击器材栏上的群延迟呼应按钮。
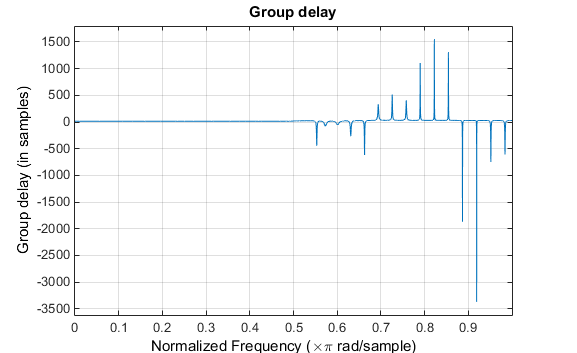
倘若咱们将此非线性相位滤波器与有正确的 14.5 个样本的群延迟的线性相位滤波器实行对照,获得的滤波器的阶数为 2*14.5,即 29。利用b = cfirpm(29,[0 0.5 0.55 1],lowpass)时,29 阶滤波器的通带和阻带波纹要大得众。这些对照能够协理您决意哪种滤波器更适合特定的使用。
请正在 MATLAB 号召行窗口中直接输入以推行号召。Web 浏览器不赞成 MATLAB 号召。
